量子哈希
密码学是一门研究编制密码和破译密码的技术科学。它涉及研究密码变化的客观规律，以应用于编制密码以保护通信秘密的编码学，以及应用于破译密码以获取通信情报的破译学。密码学的起源可以追溯到大约2000年前，而现代密码学则以数学为基础。
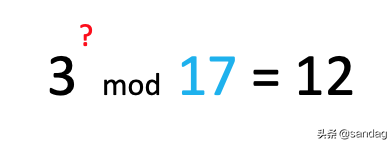
在凯撒大帝时代到上世纪70年代的很长一段时间里，密码学的发展进展缓慢，因为设计者主要依靠经验而没有运用数学原理。
重要的里程碑之一是上世纪70年代出现的RSA加密算法。RSA算法采用一种特殊的加密方式，需要两个密钥：公钥和私钥。公钥用于加密，私钥用于解密。这个算法非常可靠，密钥越长，破解难度就越大。目前已知被破解的最长RSA密钥长度是768位，超过768位的密钥尚未被破解。因此，1024位的RSA密钥可以认为是基本安全的，而2048位的密钥则更加安全。（当然，RSA也有一些缺陷，比如相对较低的效率和字节长度限制，因此在实际应用中通常会与对称加密结合使用，使用RSA加密关键内容。）
RSA算法的数学原理可以简单了解一下，其中包括离散对数问题和欧拉函数。离散对数问题是指求解一个数的多少次方模某个数等于另一个数。欧拉函数用于计算满足特定条件的整数个数。
给定任意正整数 n , 在小于等于 n 的正整数中 , 能与 n 构成互质关系的正整数个数. 复制代码
欧拉定理是一个重要的定理，它指出如果两个正整数m和n互质，那么m的欧拉函数次方减去1可以被n整除。
费马小定理是欧拉定理的一个特例，当n为质数时，欧拉函数的结果就是n-1。因此，如果两个正整数m和n互质，并且n是质数，那么m的n-1次方减去1可以被n整除。
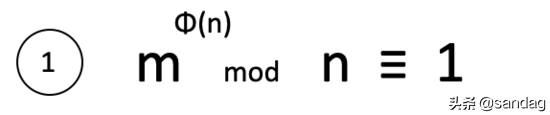
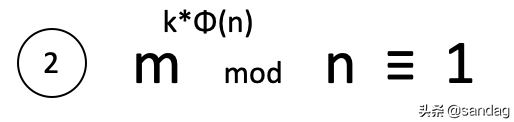
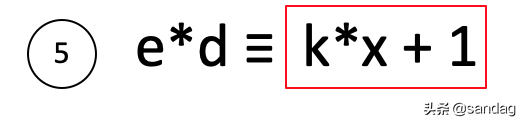
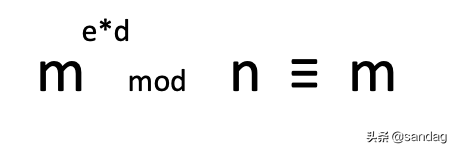
公式转换是指如果两个正整数e和x互质，那么一定可以找到整数d，使得ed-1被x整除。这个公式可以用来计算模反元素。
（其中d是e相对于φ(n)的模反元素，因为x=φ(n)。需要注意的是，公式推导的前提是m和n互质，但由于模反元素的关系，只要满足m<n，上述结果仍然成立。）
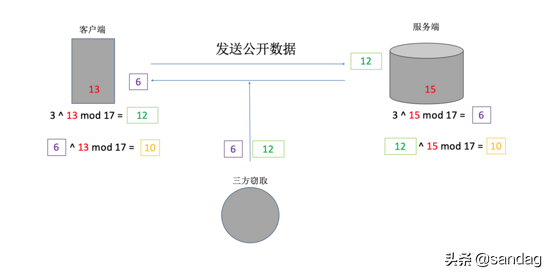
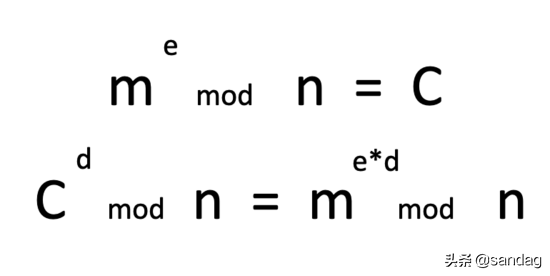
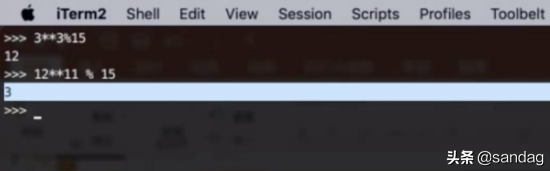
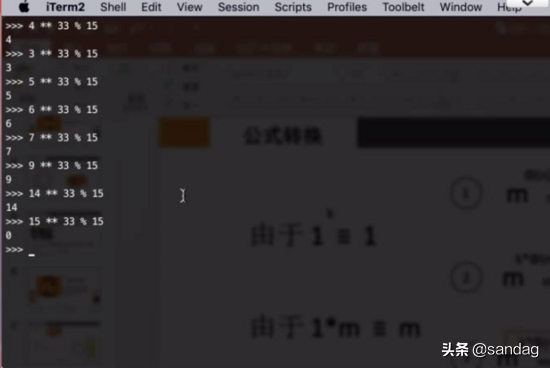
现在，让我们通过一个实际场景来了解迪菲赫尔曼密钥交换过程。根据之前的推导，我们知道（其中d是e相对于φ(n)的模反元素，因为x=φ(n)，同样，e和φ(n)是互质关系）。您可以自己尝试一下，例如m=3，n=15，φ(n)=8，e=3，d=11。
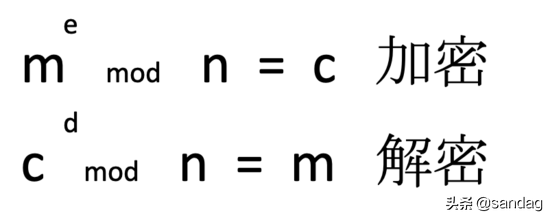
通过以上步骤，我们了解了RSA算法的原理。除了公钥使用n和e之外，其他4个数字都是保密的。
接下来，让我们介绍一下哈希算法。哈希算法是一种将任意长度的输入通过散列算法转换为固定长度输出的方法，输出结果称为散列值。哈希算法的特点是将输入压缩成较小的输出空间，不同的输入可能会得到相同的输出，因此无法从散列值确定唯一的输入值。
哈希算法主要用于数据摘要、数据完整性校验等方面。由于相同数据的哈希结果是相同的，因此存在大量的哈希结果记录数据库，这使得哈希算法变得可逆。为了增加安全性，我们常常采取加盐、嵌套哈希、动态盐和HMAC等方式对数据进行加密。
HMAC加密方案使用一个密钥进行加密，并进行两次散列。在实际开发中，密钥通常来自服务器下发给客户端，并可能根据账户绑定。为了确保接口安全，我们可以采取多种方式，如使用HTTPS进行加密、结合对称加密和非对称加密等。即使是最安全的加密算法也存在被破解的风险，因此我们需要根据实际需求来设定注册和登录逻辑，例如通过新设备授权等方式决定是否向客户端下发密钥。
以上方式可以有效防止接口被抓包的情况。用户的HMAC散列值只在注册时传输一次，抓到接口中的时间戳加HMAC散列值进行散列是很难猜出嵌套方式的。每次请求的源数据（时间戳加HMAC散列值）都不同，并且有效期只有最多1分59秒，最少一分钟（有效期可灵活控制）。因此，抓包人员抓到请求源数据后，必须在两分钟内登录，否则将失效。
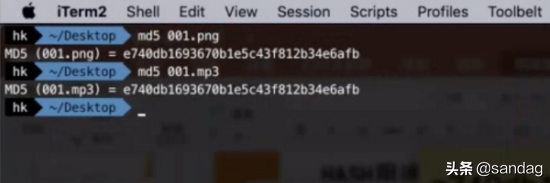
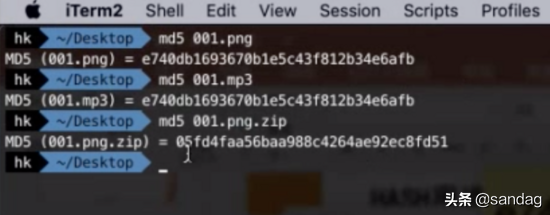
另外，关于哈希算法，有一个题外话。有时候我们可能会遇到上传到云盘的文件被和谐的情况，即使改变文件名或后缀名重新上传也不行。这就是哈希算法的一种应用场景。哈希算法对二进制数据进行散列，因此改变文件名或后缀名不会改变文件的二进制数据。
